Secure Two-Party Computation (S2PC)

Not to toot my own horn here but when I was in high school I used to be quite popular :). I was moreover one of the least shy people I know but when it came to girls, I was interested in, I suddenly turn to this timid shell of a person. This awkward version of a popular guy is not uncommon and the fear of rejection is the reason that rattles us to the core. I still remember this girl from my high school I’ve never talked to, because of that fear — let’s call her Lalla Salma in the sequel (Any resemblance to actual persons, living or dead, is purely coincidental). No matter how much courage I’ve summoned and how firmly I’ve convinced myself I don’t care about the outcome, hearing no from Lalla Salma would have hurt. A graceful no hurts a great deal less but a cruel no in public drives a knife through the male psyche.

Growing up, I became a cryptographer and figured out a mathematical way to deal with such a situation. How can you make secure advances to Lalla Salma ? Is there a way to securely guess the outcome ? or simply put, how can you avoid a dismissive no in public ? The solution uses Yao’s Garbled circuits for secure two-party computation (S2PC).

Given private inputs $x$ and $y$ and a public function $f$, this method enables two parties to securely compute the outcome $f(x,y)$ without revealing the secrets $x$ and $y$. A circuit is just a way to represent a computation consisting of just operations on bits, like AND, OR, NOT and a garbled circuit is a way to “encrypt a computation” that reveals only the output of the computation, but reveals nothing about the inputs or any intermediate values. Our situation makes the basic way to understand how the protocol works. Let the secret $x$ be 1 if I am interested in Lalla Salma and 0 otherwise. Similarly, her secret $y$ is either 1 or 0. We want to securely compute a function that outputs 1 if we both are interested in each other and 0 otherwise — no one should be able to guess the inputs. A simple function would be an AND gate.

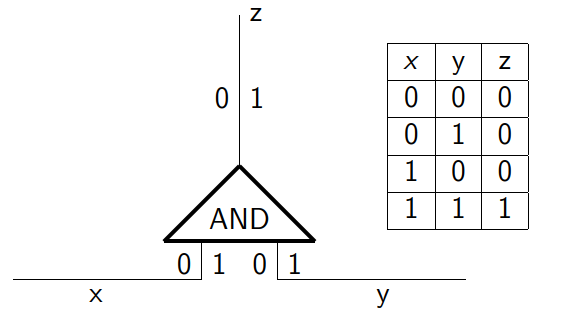
There are 4 possibilities in the truth table but only one is the actual reality. Next, we “garble” this circuit as follows: For each wire $x, y$ and z, we specify two random values corresponding to 0 and 1 and then we encrypt (using some symmetric cipher such as AES) the truth table by encrypting the output-wire key with the corresponding pair of input-wire keys. Which results in the Garbled Computation Table (GCT).

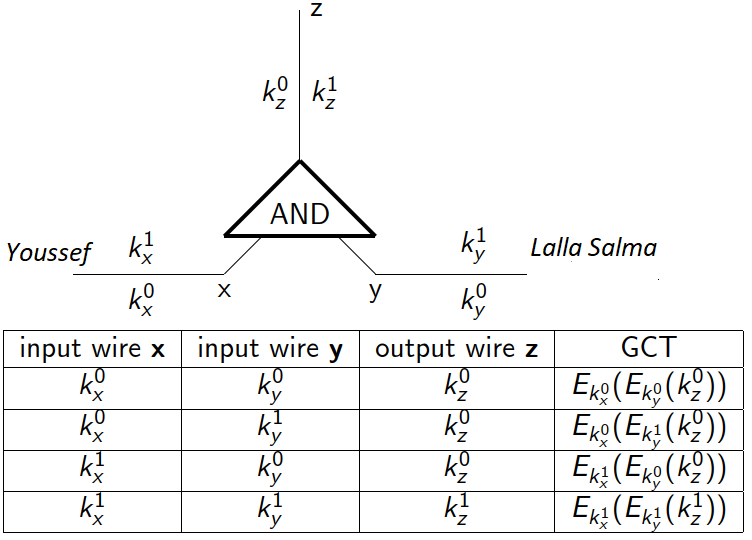
Given two input keys only one row of the GCT can be decrypted correctly. Next, we rearrange the GCT — so that no information is leaked — and send it to Lalla Salma along with my input key. Note that, since the key is random, there is no way to associate it with the actual bit. At this point, she has the GCT and my input key but needs the key I have already associated to her input bit. But just like me, Lalla Salma doesn’t want to reveal her secret (bit)! Neither want I to send her both keys, as she would be able to decrypt more than a GCT row. What we need here is a protocol in which a sender transfers one of potentially many pieces of information to a receiver, but remains oblivious as to what piece has been transferred. Fortunately, such a protocol exists and is called 1-out-of-2 oblivious transfer (OT). In the next section, I will present a simple 1–2 OT protocol but if you don’t know how RSA encryption works just skip this section since explaining it goes beyond the scope of this post.

1–2 Oblivious Transfer

• Alice holds $m_0, m_1$, and an RSA key pair $(e, d, N)$. Bob holds the public key $(e, N)$ of Alice, $x \in {0,1}$ and wants $m_x$
• Alice generates random $x_0, x_1$ and sends them to Bob
• Bob chooses a random $k$, computes $v=y_x+k^e$ and sends $v$ to Alice.
• Alice computes $k_0=(v-x_0)^d$ and $k_1=(v-x_1)^d$, and sends $m_0'=m_0+k_0$ and $m_1'=m_1+k_1$ to Bob
• Bob computes $m_x=m_x'-k$ and learns nothing about $m' _{1-x}$

Now, using 1–2 OT protocol, Lalla Salma can have her input key without me knowing anything about her secret bit. At this point, we can decrypt the GCT row corresponding to our secrets and reveal securely the output value. If it is a 0, none is able to tell who rejected the other and if it is a 1… Jackpot!

By and large, this is how we can do secure two-party computation. So, dear Lalla Salma, if by any chance you’re reading my post, here is my secret key ;)

0x3361736861206c6d616c69696969696b