Shamir Secret Sharing — The magic 3S Spell

“There are no more Horcruxes. It’s just you and me. Neither can live while the other survives, and one of us is about to leave for good…” —Harry Potter and the Deathly Hallows, Chapter 36: The Flaw in the Plan.

The Horcrux hunt was a mission started by Albus Dumbeldore and given to Harry Potter to find all of Lord Voldemort’s remaining Horcruxes and destroy them. Obsessed with immortality from a young age, Lord Voldemort created a series of Horcruxes in an effort to prevent his death. A Horcrux is a vessel into which one places a piece of one’s soul to protect one from mortal death. Voldemort split his soul into 7 secret parts in a way that reconstruction is possible. It is widely believed that the process for Horcrux splitting involves a spell and a horrific act is performed after a murder has been committed, but this is not true. Voldemort invented this cover story to keep secret the very simple spell he used (a wizard patent for the technical term) — it is called the 3S spell.

The 3S spell is nothing but a Shamir secret sharing scheme. In this scheme, a dealer (Voldemort) splits a secret (his soul) into multiple shares (Horcruxes) in a way that reconstruction is only possible when combining all of the shares or some sufficient fixed number of them. The spell uses some basic polynomial algebra magic (1st year at Hogwarts) and some finite field wizardry.

Basic scheme

Let’s $s$ be the secret and $n$ the number of shares, a dealer can construct a secret sharing scheme where only $t < n$ custodians can reconstruct the secret $s$. He first generates a $t$-degree polynomial $P(X) = p_0 + p_1X + p_2X^2 + · · · + p_t X^t$ where $p_0$ is the secret $s$ and $p_1, p_2, \dots , p_t$ are chosen at random from the finite field we’re working in (e.g. $\mathbb{F}_31$ which means integers from 0 to 30). He then computes the points $v_1 = P(1), v_2 = P(2), \dots and v_n = P(n)$ and distributes these $n$ shares to the custodians. Any $t < n$ shares can reconstruct the polynomial $P$ with interpolation (e.g. Lagrange interpolation) and recover the original secret $s = P(0)$. Note that any $t − 1$ shares would interpolate with high probability a false polynomial.

Verifiable scheme

There are two problems with the basic scheme:

• A malicious custodian can submit a false share
• A malicious dealer can distribute false shares

The first issue can be addressed by adding some fingerprint to the secret. This way, if a malicious custodian submit a false share, the reconstructed secret won’t be correct and the fingerprint lost. One way to do this is by concatenating the secret s with the hash of the last 31 bytes of s, i.e. s ← (s||sha256(s[: −32]). However, identifying the malicious custodian remains impossible in this approach.

The solution to the second problem, can both identify a malicious dealer and a malicious custodian in the first scenario. A simple approach would be to publicly publish the hashes of shares but this might be impractical in some use-cases where the number of custodians increases quickly. In fact, each custodian will have a database of auxiliary information that may increases quickly over the time. A better approach was proposed by Feldman and uses homomorphic commitments.

Feldman’s approach:

In this approach, the dealer publishes the commitments of polynomial’s coefficients $p_0= s$ and $p_1, p_2, \dots, p_t$ that are homomorphic with respect to multiplication. Such a commitment is known to be a Pedersen’s commitment. Given a finite field of prime characteristic $p$ and a generator $g$, the dealer publishes $c_0 \equiv g^s \pmod p, c_1 \equiv g^{p_1} \pmod p, \dots$ and $c_t \equiv g^{p_t} \pmod p$. Given the commitments $c_i$ for $i \in [0, t]$, the is no way to retrieve the secret $s$ and the coefficients $p_1, p_2, \dots, p_t$ because of the hardness of the discrete logarithm problem. A custodian can verify that the share $v_i$ he was given by the dealer wasn’t tampered with thanks to the homomorphic property of Pedersen’s commitments. In fact,

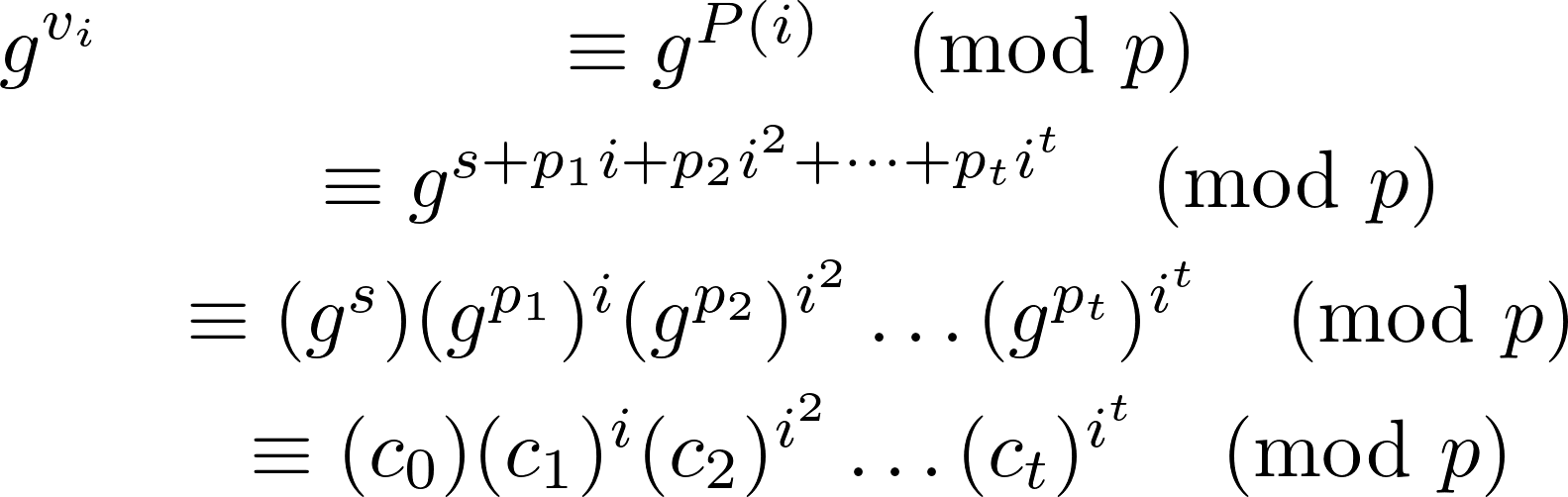
This is basically the magic 3S spell that allowed Lord Voldemort to split his soul into 7 horcruxes. The process is rather simple that even Ronald Weasley can perform, but Tom Riddle invented the horrific-act-after-murder story to keep away wizardry newbies from reaching immortality.

Yes, I ruined your childhood memories. Sorry Not Sorry.