Why do we use elliptic curves for cryptography?

In the series of posts I am willing to write, I will try to answer technical questions I have been asking myself throughout my readings about Maths, cryptography and Blockchain. For many questions, I couldn’t find easily or completely the answer I was looking for. One of these questions I faced is: Why did we even consider using elliptic curves for cryptography ? The question is “Why” rather than “How”. Elliptic curves are mathematical objects from the algebraic geometry and one should be normally surprised when discovering that such objects are used to encrypt data. In fact, elliptic curves are non-singular algebraic curves satisfying an equation of the form $y^3=x^3+ax+b$ (cf. figure 1).

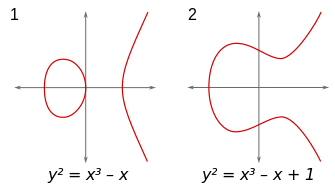
Well, that doesn’t help us a lot.. And since I started this post with a question you have the right to ask more questions: What do these mathy words mean? How did we get this equation? And why are they even called “elliptic” even though they do not resemble “ellipses” in any way ? Don’t worry I’ve asked myself these same questions and we’re going to deep dive into the answers in later posts. For now, let’s go back to the main question: Why do we use these curves to encrypt data? To answer this we have to trace the evolution of cryptography over the years. The earliest known cryptographic schemes use a symmetric approach — that is using the same key for both encryption and decryption. A simple example of this approach and one of the oldest would be “Caesar cipher” in which each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet. In this scheme the encryption/decryption key is the fixed number of positions that must be kept secret and known only to the communicating parties. This symmetric approach is still widely used today through many ciphers such as AES, Blowfish or RC4 but the requirement of a secret symmetric key is still the main drawback. Cryptographers have been then looking for innovative asymmetric approaches where the decryption key differs from the encryption one. That is said, they have been looking for algorithms where it is easy to derive the decryption key (public) given the encryption key (private) and difficult the other way around — or mathematically put, a function that is straightforward to compute and computationally hard to inverse. One of the first algorithms proposed and still widely used nowadays is the famous RSA which relies on the hardness of the “factorization problem”. In fact, given two prime integers, it is easy to compute their multiplication but presumably hard to find the prime integers given the multiplication output. At this point you may (should) be asking why is it hard to factorize an integer and the answer is that there is no published algorithm that can do this in polynomial time (an algorithm is said to be of polynomial time if its running time is upper bounded by a polynomial expression in the size of the input for the algorithm). In fact, the best published asymptotic running time (on a classical computer, not a quantum one. Wait, quantum?) is for the general number field sieve (GNFS) algorithm which has a sub-exponential complexity. In short, integer factorization is “hard” in the sense of computational efficiency because we haven’t found just yet a reason for it to be easy, and we can’t prove it is hard. All this to come to the point that integer factorization, in my opinion, has nothing to do with the unknown primes distribution as widely believed. It is true that the problem is built upon the fundamental theorem of arithmetic which states that every integer can be uniquely represented as the product of prime numbers but I think that the chaotic nature of primes distribution has no bearing on the problem. There’s no reason to expect that factorization would become even a bit easier by proving the Goldbach conjecture, the twin primes conjecture or the Riemann Hypothesis for examples. However, the problem becomes computationally easier (polynomial time) when using quantum computers to run Shor’s algorithm as we will see on a later post. Another proposed asymmetric construction relies on the hardness of the “discrete logarithm” problem in cyclic groups. Given integers a and b in a carefully chosen group G, no efficient method is known for recovering the integer k such that $a=b^k$. In fact, the problem is quickly computable in a few special cases but in some cases there is not only no efficient algorithm known for the worst case, but the average-case complexity can be shown to be about as hard as the worst case using random self-reducibility. So choosing the group G is critical and a popular choice that provides good security assumptions is large prime order subgroups of groups ${\mathbb{Z}}_p$. These groups were used to build several known cryptographic protocols such as ElGamal encrytpion, Diffie-Hellman (DH) key exchange and Digital Signature Algorithm (DSA). However, using these groups requires large key sizes because of the sub-exponential GNFS algorithm as well. In fact, while computing discrete logarithms and factoring integers are distinct problems, both are special cases of the hidden subgroup problem for finite Abelian groups and thus, for both, the most efficient approach remains GNFS on a classical computer and Shor’s algorithm on a quantum computer. At this point, you may be thinking that somehow changing that group G from finite fields to elliptic curves may provide better security assumptions. You’re right! The best published algorithms to find discrete logarithms over elliptic curves are Pollard’s $\rho$ or baby-step-giant-step with a way better running time than GNFS. But wait, what is a discrete logarithm over elliptic curves? (you ask a lot of questions, huh?) Well, no worries, we will soon deep dive into all the machinery ;)