Why elliptic curves are called "elliptic" ?

Every name tells a story. If you ask new parents “how did you choose your baby’s name?” sometimes the response will be a vague “Oh she chose!” but most of the time there is a story behind, and it’s often a great story about going through dozens of possibilities until one clicked. It goes from her favorite fictional character to her favorite great-aunt, so the baby has to be called Khaleesi. Obviously. In mathematics, it is no different. When mathematicians introduce their new baby to the world, they choose an appropriate name far from being random. In my last post, I have talked about elliptic curves and why they are used in cryptography. This triggered the question on why they are called “elliptic” even though they do not resemble ellipses in any way.

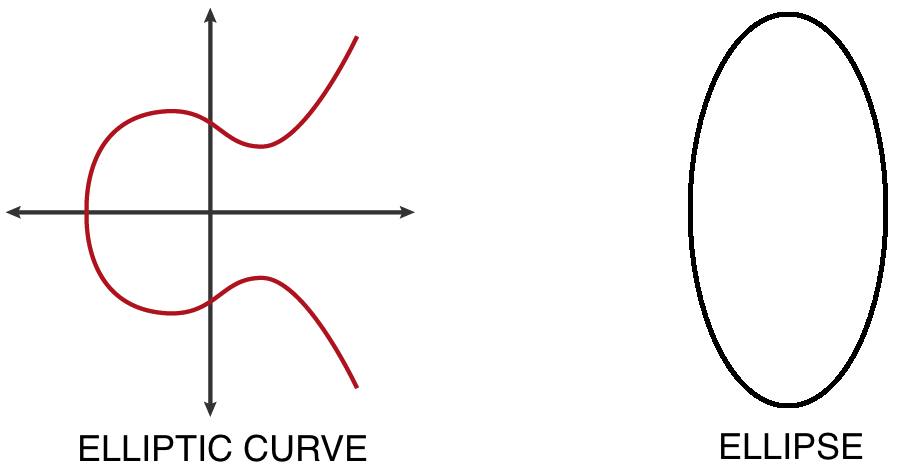
Elliptic curves are of cubic equations $y^2=x^3+ax+b$ while ellipses are of quadratic equations $x^2/a^2+y^2/b^2=1$. So, prima facie, there is no connection between them. But looking deeply into the history of elliptic curves, one finds out the connection. In the 18th century it was natural to ask about the arc length of an ellipse. In fact, despite their similarity to circles, ellipses are quite different. For example, a circle’s circumference is given by $2 \pi r$ and its area by $\pi r^2$ where $r$ is the radius. It is remarkable how the constant $\pi$ relates the circumference to the area given the radius $r$. But things are not that easy when dealing with ellipses. Given $a$ and $b$ as the semi-radii, the area of an ellipse is $\pi ab$ but the circumference is a more difficult question. More generally, the arc length of ellipses is difficult to calculate and is given either by a hard integral or by a rather formidable series. This question led to the study of $\sqrt{f(x)}$ where $f(x)$ is a polynomial of degree 3 or 4. These functions cannot be described with familiar calculus functions and came to be known as elliptic integrals. For circles, $f(x)$ is a quadratic polynomial and we get “circular integrals” which are easy to handle. for example, we know that $\int dx / (\sqrt{1-x^2}) = \sin ^{-1} (x)$ and the inverse of the function, namely $\sin{x}$, is well studied and easy to deal with. Thus, circular integrals lead to the periodic trigonometric functions. Similarly, studying the inverse of elliptic integrals leads to some doubly periodic functions which came to be known as elliptic functions (let’s call them ℘(z) in the sequel, because ℘ looks nice). Furthermore, all the derivatives are doubly periodic with the same periods and satisfy a cubic differential equation. Now in calculus, you learn about parametric equations and how they can describe a curve. By a parameterization of a curve $C$, we mean a continuous bijection from a set of numbers to the set of all points on $C$. For example, letting $x=a \sin{t}$ and $y=b \cos{t}$ with $t \in [0, 2 \pi)$ gives a familiar parameterization of the standard ellipse $x^2/a^2+y^2/b^2=1$. In the same way, we see that setting $x=℘(z)$ and $y=℘’(z)$ gives a parameterization of the cubic curve known today as an elliptic curve. Names are reservoirs of stories and this was the story behind elliptic curves’ name.

One last thing before I forget, dear future son, if this post lives long enough so that you are reading it now, I am sure you will understand why I called you Jon Snow. But for now, you know nothing Jon Snow.